logo

Please Wait...

  • home-2-slider
    MATHEMATICS BEHIND THE TEXTBOOKS
    WHY AND HOW DOES VARIOUS FORMULAS WORK?

Logarithmic Inequalities: problem I $$\log_{\frac{1}{4}}x < 1 $$

answer
Solution 1
Solution 2
Challenge
For teachers

$$\log_{\frac{1}{4}}x < 1 \Leftrightarrow x \in (\frac{1}{4},\infty) $$

Solution 1
Substitute number on the right side by a logarithm, change inequality, and then ignore logarithms on both sides.

1. Substitute number on the right side by a logarithm with the base 1/4.

answer
help

Do you remember definition of a logarithm ?

Logarithm itself just finds the power to which the base must be raised to produce some given number :

Problem 1 - Graph of a logarithmic function

In our case, we have the base (1/4), we have the power (1) and we are searching for a "given number". The question is then slightly changed : If I power our base (1/4) to number 1, what number do I get?

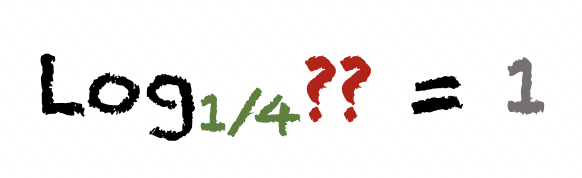
Problem 1 - Graph of a logarithmic function

If you need more help, this link may help you or google "definition of a logarithmic function ".

$$\log_{\frac{1}{4}}x < \log_{\frac{1}{4}}\frac{1}{4} $$

2. Change inequality and ignore logarithms.

Do you know why we can use this "trick"?.

It is crutial to understand this step because it sometimes works and sometimes does not! If you are not sure, just follow the "help" button.

answer
help

1. Look at the graph of a logarithmic function with the base 1/4.

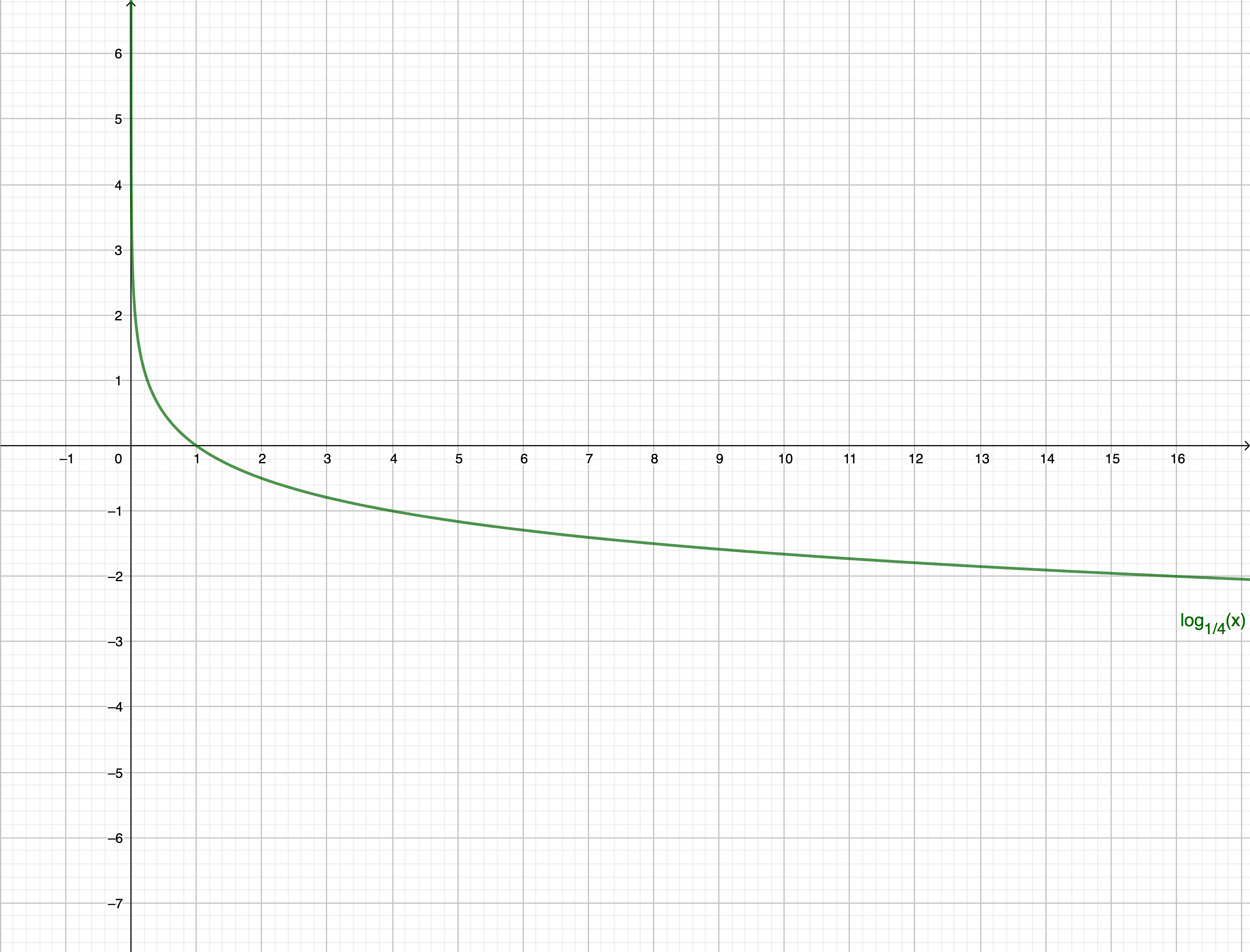
Problem 1 - Graph of a logarithmic function

Try to create the graph by yourself. You can do it in a classic way, using just a pen and a paper, or you also can use an online editor (simple and free one is e.g. GeoGebra ). If you need more help, this link may help you or google "basic graph of a logarithmic function".

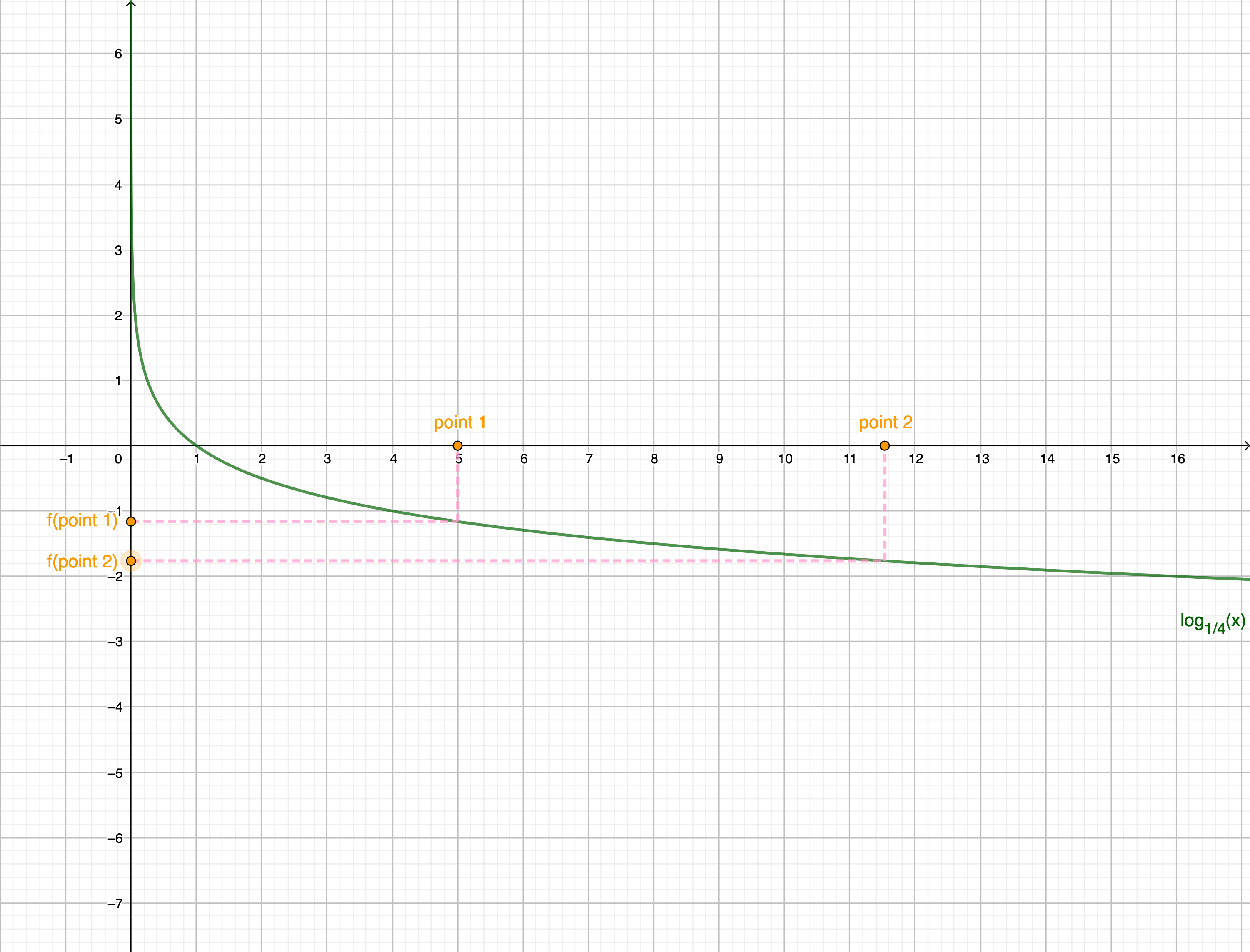
2. Pick up any two points on your graph.

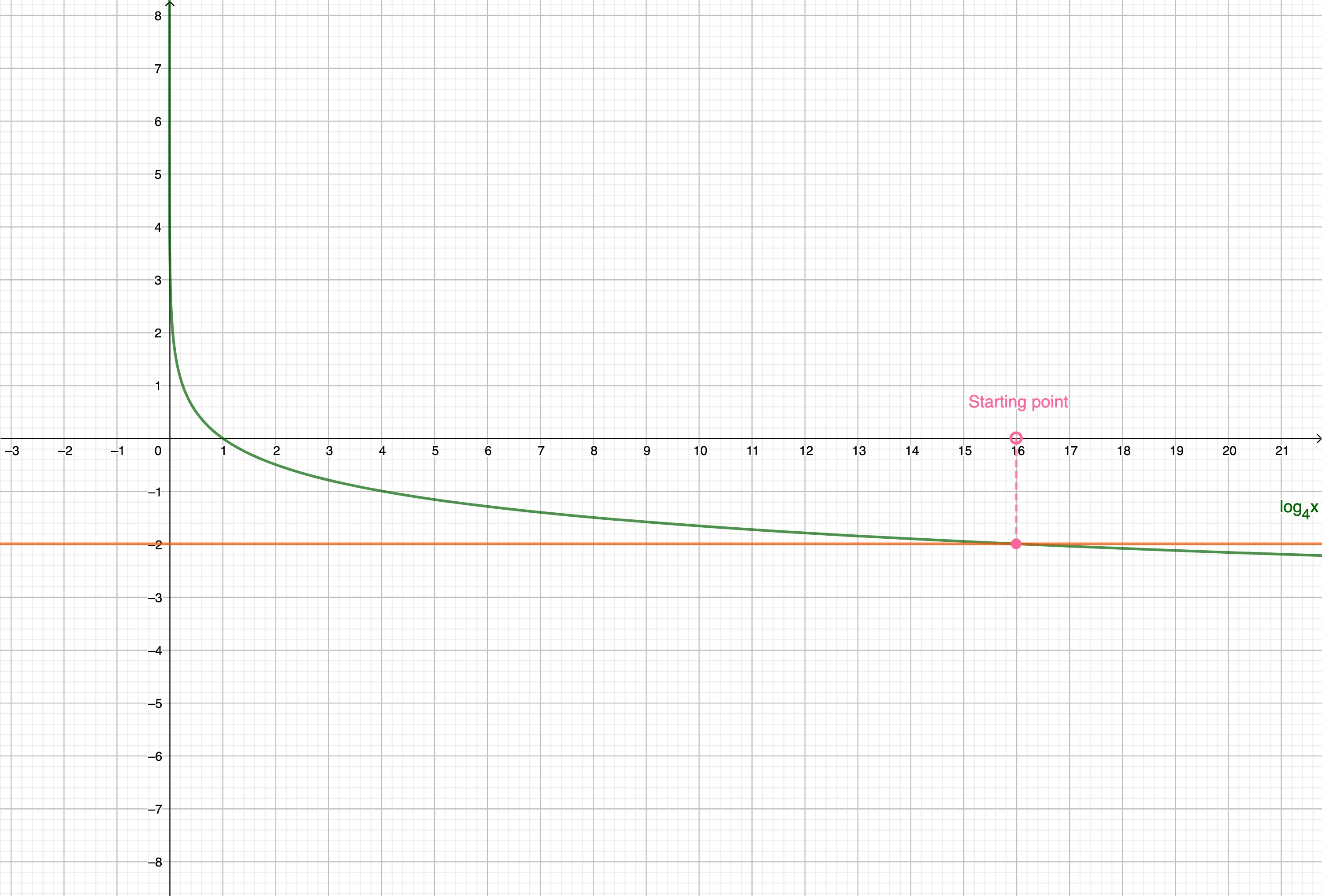
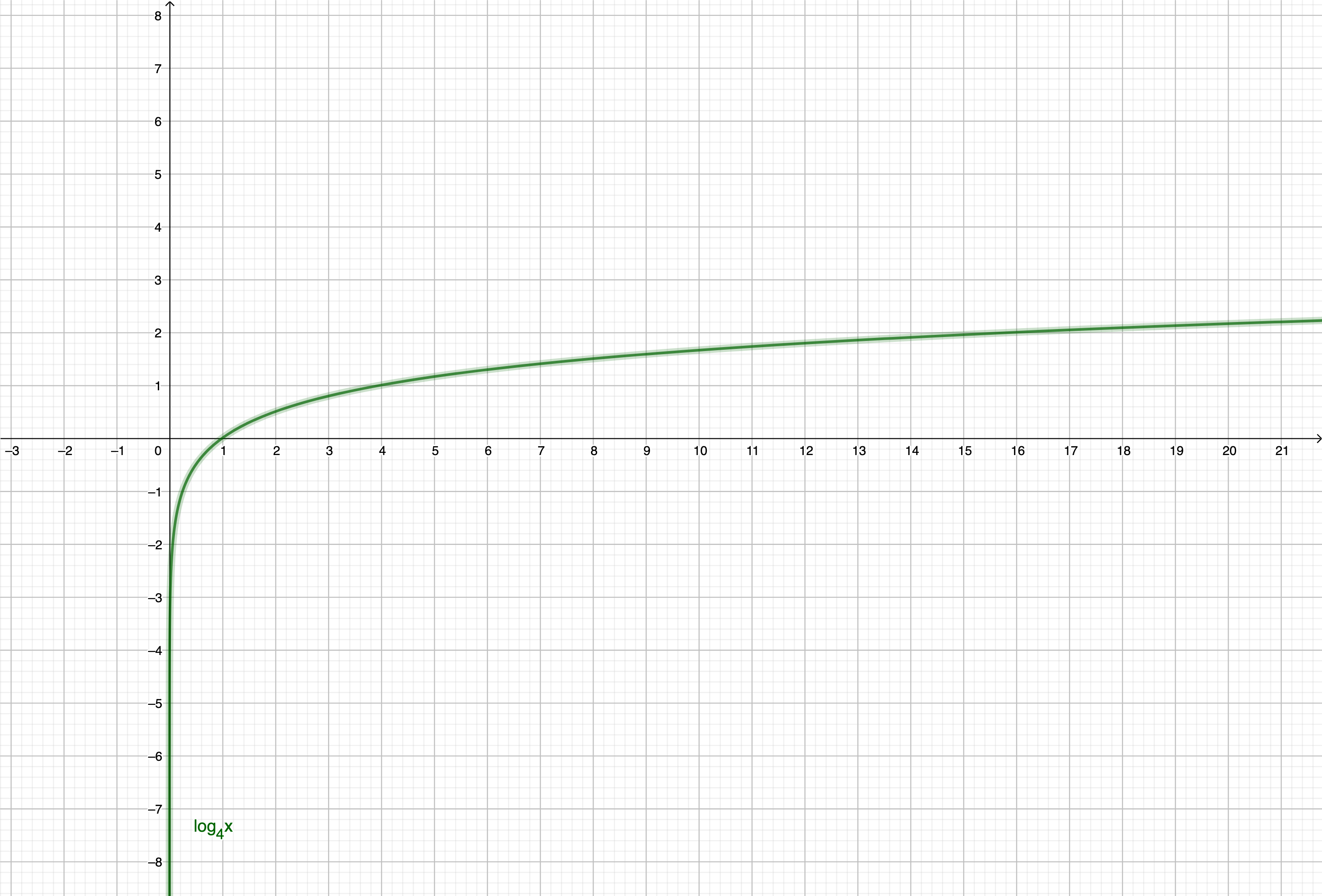
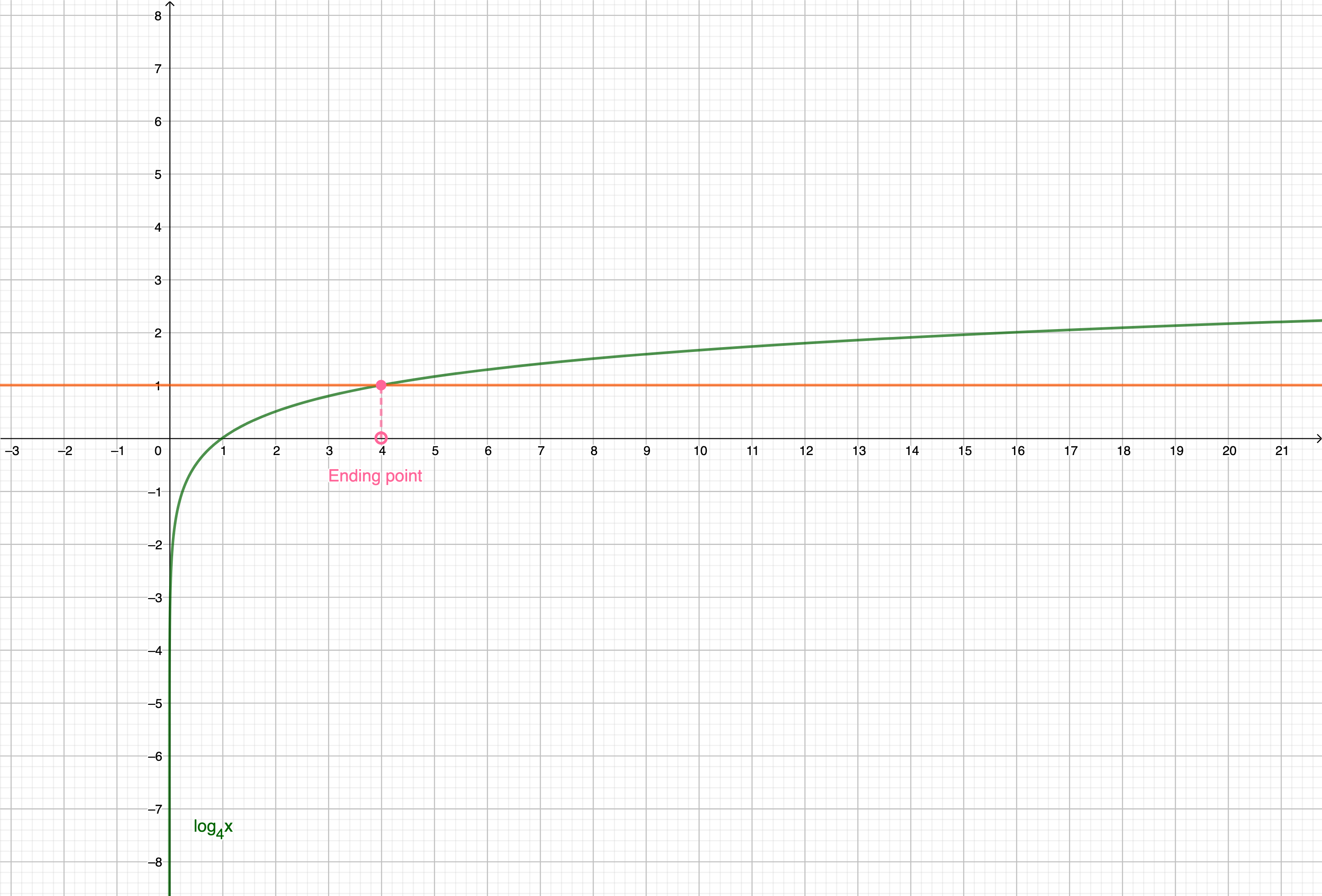
Example 1: Problem 1 - Graph of a logarithmic function

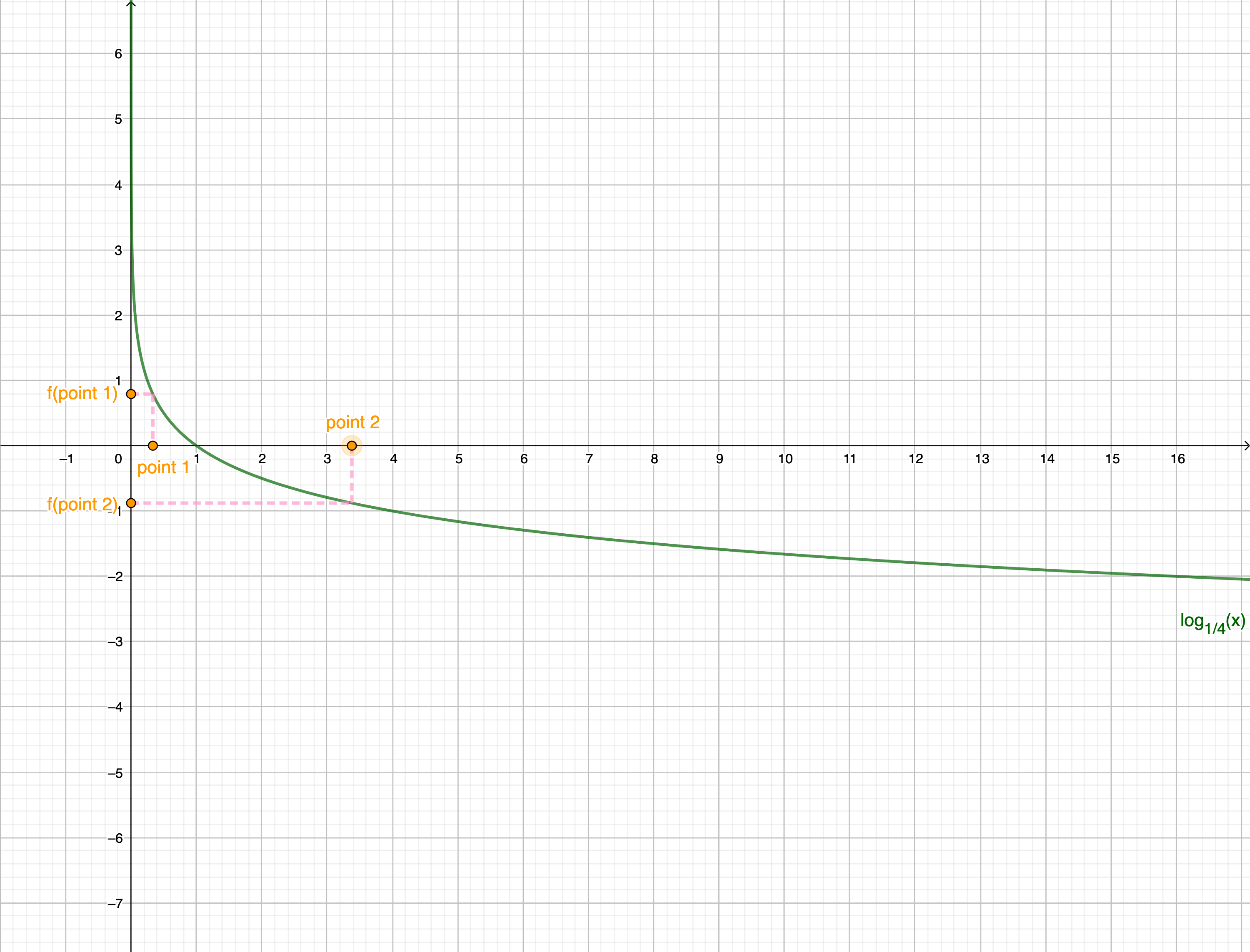
Example 2: Problem 1 - Graph of a logarithmic function

3. Now, think about the relationship between these points and its functional values.

If the functional value in the point 1 is greated than the functional value in the point 2, how is the relation between the point 1 and the point 2?

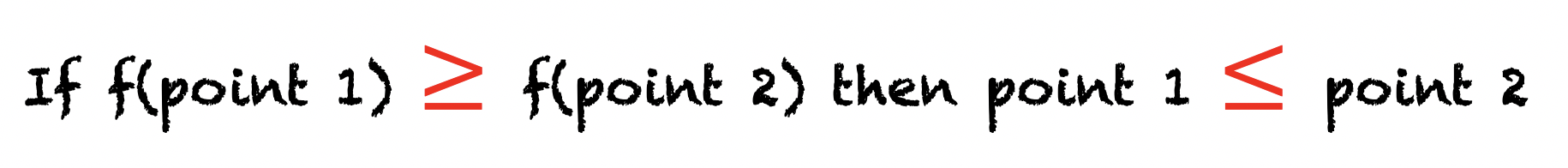
Relation between points and its functional values of a logarithmic function

4. "Functional value" is just the different name for a logarithm (in this our case).

Relation between points and its functional values of a logarithmic function

Looking at this relation we can see, that if we have the logarithmic inequality of two logarithms with the same base, we do not have to work with logarithms. It is enough to work with "the points". In other workds, we just have to change the inequality and then we can ignore logarithms.

5. Is the relation same for any logarithm ?

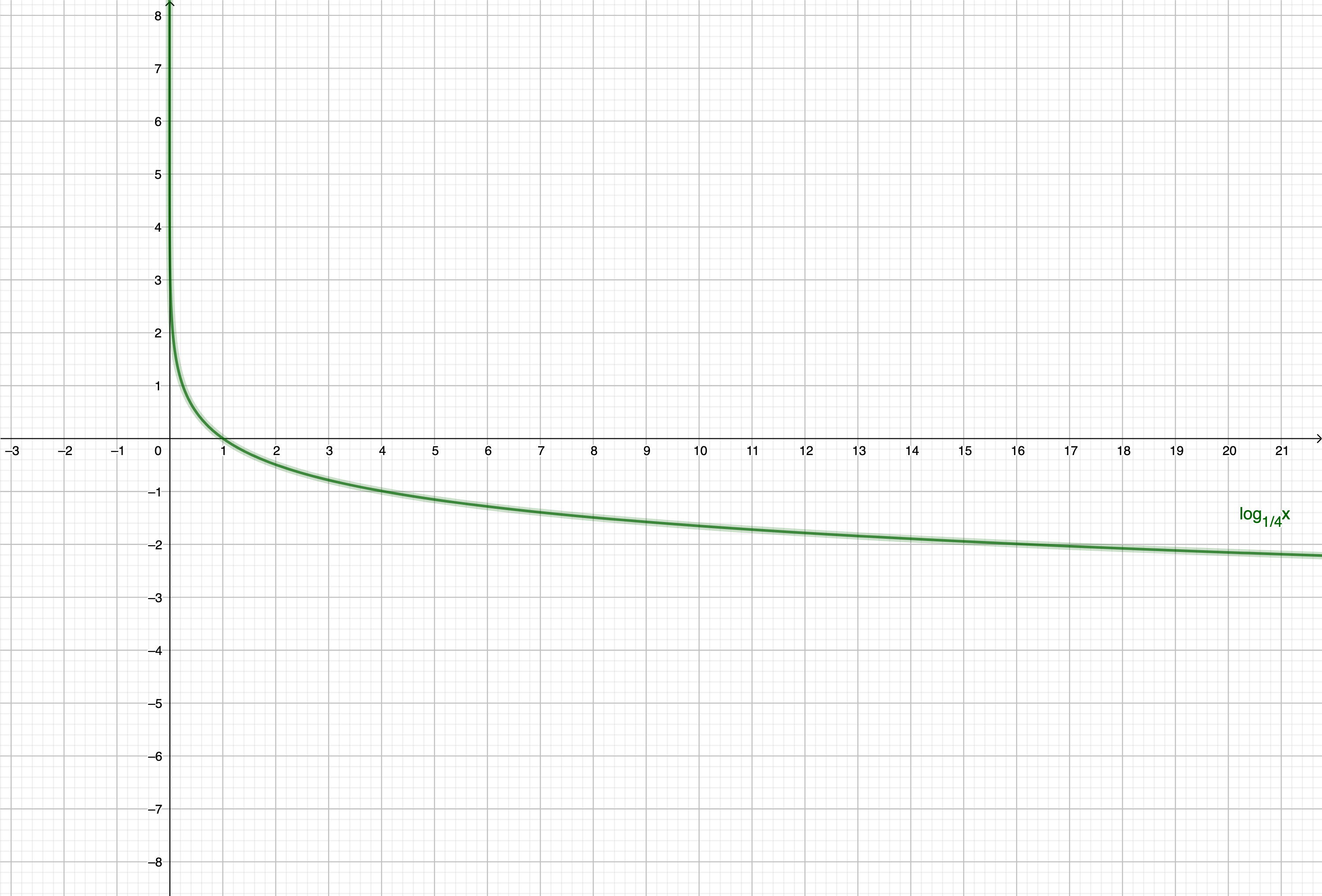
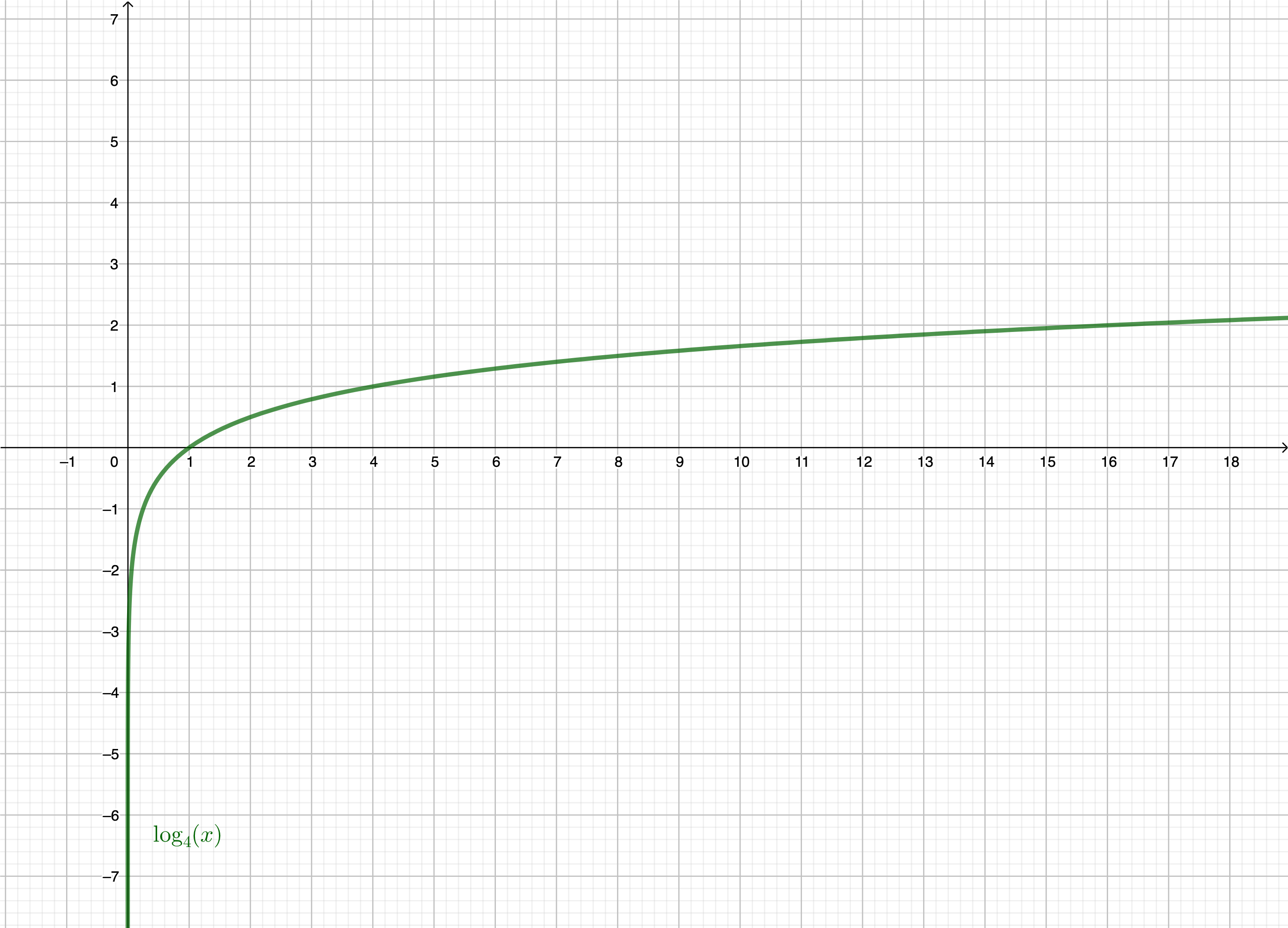
Try to figure it out by yourself. Think about different logarithms. Take e.g. logarithm with the base 4. How does its graph look like? How is the relationship between two points and its functional values at this graph?

No! It depends on the base of a logarithm.

Look at the graph of a logarithm with the base 4:

Logarithm with the base 4

Logarithm with the base 4

Relation between points and its functional values of a logarithmic function with the base 4

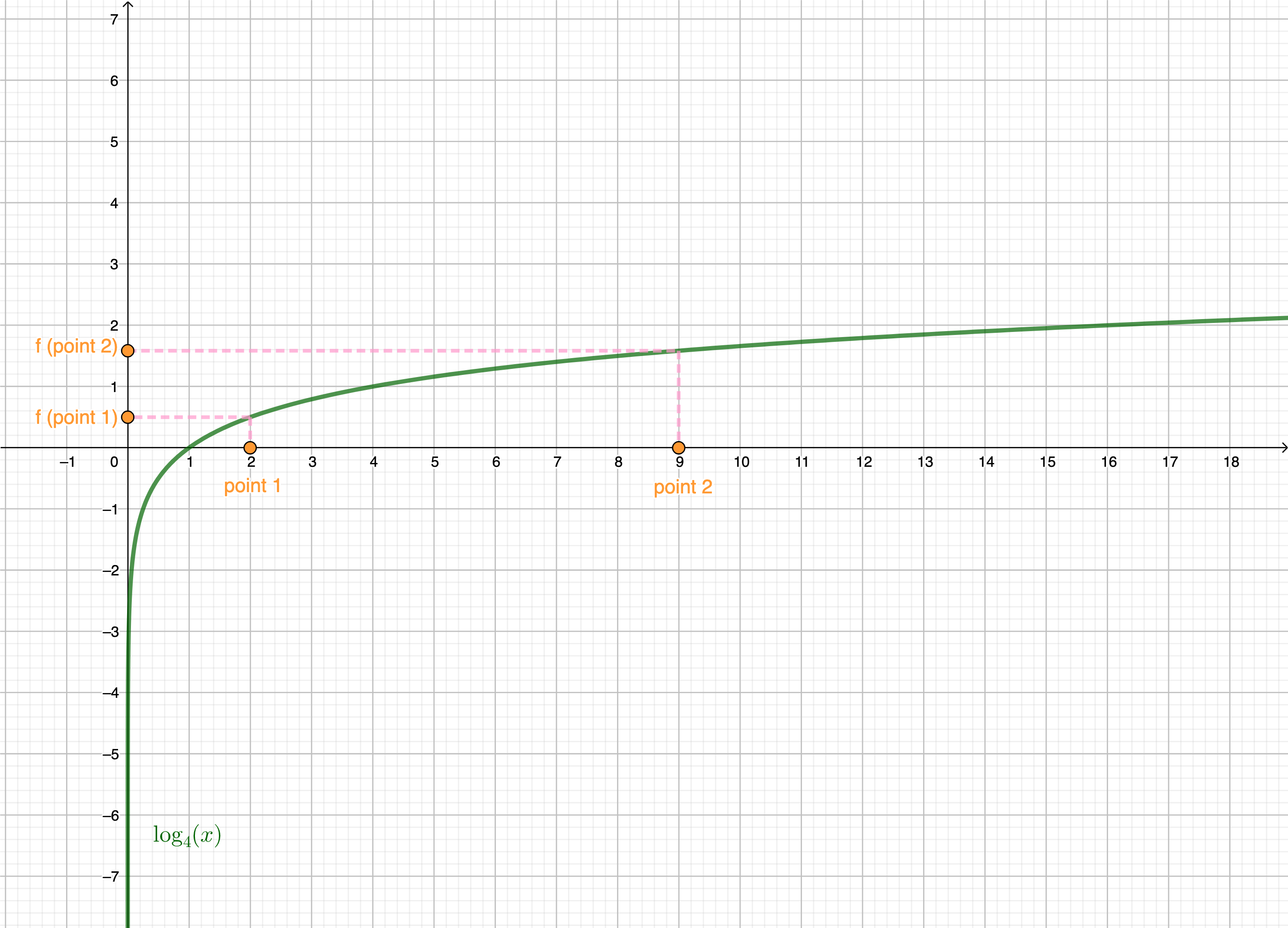
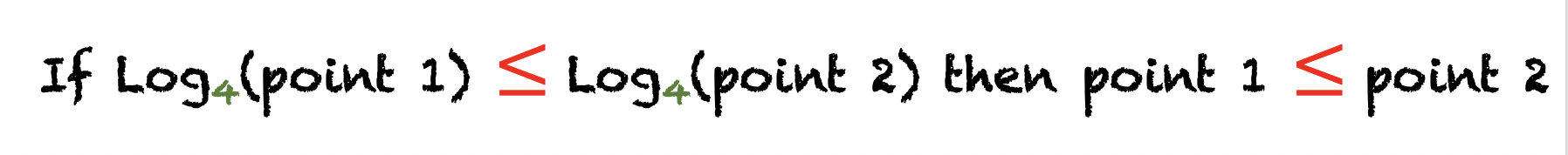
6.Conclusion, your own "tricks" that always work :)

Remember, always menas only if your inequlity has just logarithms with the same base on both sides!

Trick 1 : If the base of your logarithm is greater than 1, you can ignore logarithms.

Trick 2 : If the base of your logarithm is lower than 1, you have to change inequality and then you can ignore logarithms.

$$ x > \frac{1}{4} $$

3. Voila! You have a solution. Just summarize it through the interval.

answer
help

Interval

$$ x \in (\frac{1}{4},\infty) $$

4. Is my solution correct?

answer
help
text text

yes, it is

5. Challenge Yourself! Try to solve similar problems

mmmm
Challenge
Challenge yourself! Solve similar probles to deepen and test your understanding.
$$\log_{\frac{1}{4}}x < -2 $$
Back to the Content Map Next problem: problem II

Solutions

Problem I: Challenge 1

$$\log_{\frac{1}{4}}x < -2 \Leftrightarrow x \in (16,\infty) $$

Problem I: Challenge 2

$$\log_{4}x < 1 \Leftrightarrow x \in (0,4) $$

Problem I: Challenge 3

$$ log_{\frac{1}{4}}x \geq 1 \Leftrightarrow x \in (0,\frac{1}{4}) $$

Helpers

Problem I: Challenge 1

Look at the graph of our logarithmic function. Which x-es can I put into our inequality so, that its functional values are less than -2?

Problem 1 - Graph of a logarithmic and a constant function
Problem I: Challenge 1

Substitute number -2 by logarithm.

$$\log_{\frac{1}{4}}16 = -2 $$

When and Why can we work with the inequlity just without logarithms?

$$\log_{\frac{1}{4}}x < \log_{\frac{1}{4}}16 $$

Problem I: Challenge 2

Try to create the graph of a new logarithmic function.

Problem 1 - Graph of a logarithmic function

Now, look at the graph. Which x-es can I put into our inequality so, that its functional values are less than 1?

Problem 1 - Graph of a logarithmic and a constant function
Problem I: Challenge 2

Substitute number 1 (from the right site of our inequality) by logarithm.

$$\log_{4}4 = 1 $$

When and Why can we work with the inequlity just without logarithms?

$$\log_{4}x < \log_{4}4 $$

Problem I: Challenge 2

Go back to the graph of our logarithmic function. Which x-es can I put into our inequality so, that its functional values are greater or equal than 1 ?

Problem 1 - Graph of a logarithmic function
Problem 1 - Graph of a logarithmic function
Problem I: Challenge 3

Substitute number 1 (from the right site of our inequality) by logarithm.

$$\log_{\frac{1}{4}}\frac{1}{4} = 1 $$

When and Why can we work with the inequlity just without logarithms?

$$\log_{\frac{1}{4}}x \geq \log_{\frac{1}{4}}\frac{1}{4} $$

Forum

We are preparing a new forum for you!

If you have any questions or if you need any help, I will be glad to help you! Please feel free to send me an email (martina.babinska.sk@gmail.com).